Een roosterpunt is een punt P(x, y) in het vlak waarbij x en y gehele getallen zijn.
Zo is bijvoorbeeld het punt A(2,3) zichtbaar vanuit de oorsprong O(0,0)
maar de punten B(4,6) en C(-3,-9) niet
omdat ze worden 'afgeschermd' door het punt A.
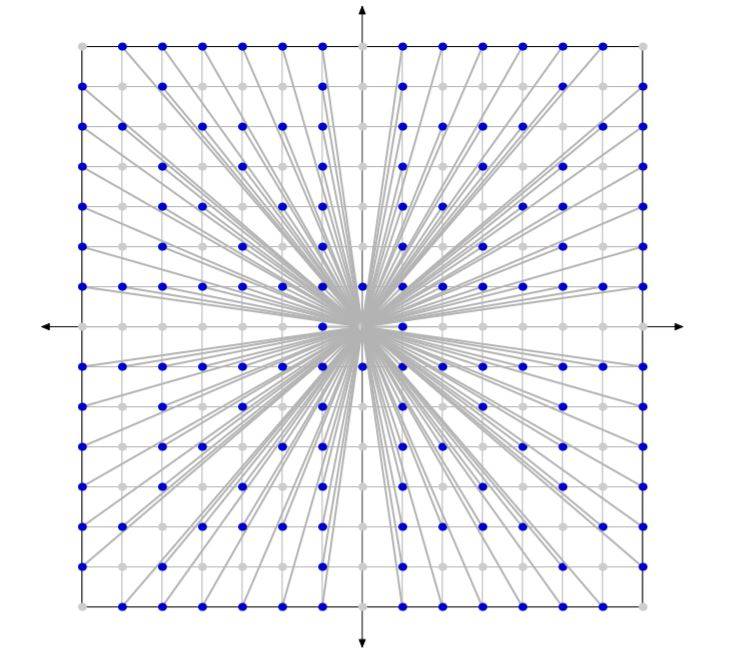
Op de bovenstaande figuur zijn de blauwe roosterpunten zichtbaar vanuit de oorsprong en de grijze niet.
Een roosterpunt is bijgevolg zichtbaar vanuit O als zijn twee coördinaatgetallen x en y onderling ondeelbaar zijn
(een doordenkertje!).
Nu is de kans dat twee willekeurig gekozen gehele getallen onderling ondeelbaar zijn gelijk aan 6/π².
Dit is een direct gevolg van een geniale formule van Euler
die had ontdekt dat er een verband bestaat tussen de Riemann-zèta-functie en priemgetallen.
Je leest alles hierover in de Engelstalige bijlage.


Maak jouw eigen website met JouwWeb