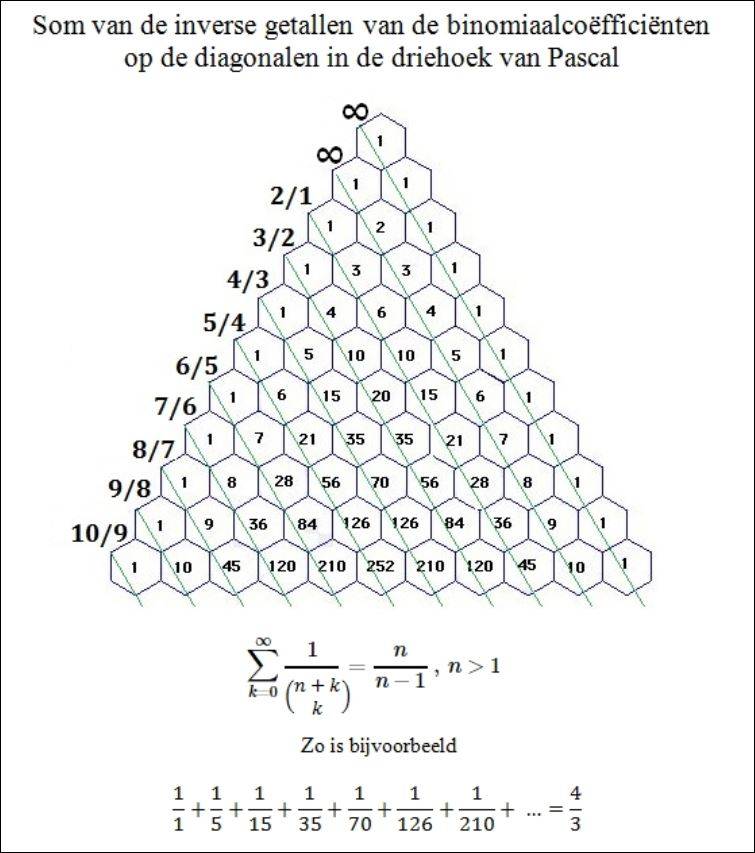
Als je de inverse getallen neemt van de binomiaalcoëfficiënten op de tweede diagonaal (van boven te beginnen)
bekom je de welbekende harmonische rij met de eigenschap dat de som van de termen
1 + 1/2 + 1/3 + 1/4 + ... divergeert naar oneindig.
Zie bv. https://en.wikipedia.org/wiki/Harmonic_series_(mathematics).
Maar wat is de som van de binomiaalcoëfficiënten op de andere diagonalen?
Het resultaat staat hieronder en voor een bewijs verwijzen we naar
https://www.cut-the-knot.org/arithmetic/algebra/BinomialReciprocalsInPascal.shtml .
En ook dit verband kan je wellicht verbazen:

BEWIJS.
Bereken de bepaalde integraal van (1 – x)n in het interval [0, 1] op twee manieren:
via substitutie en na toepassing van het binomium van Newton.


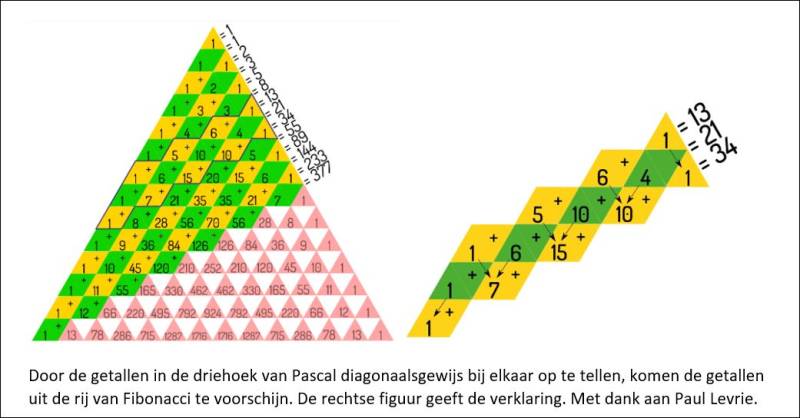
Maak jouw eigen website met JouwWeb